Übung Aufgaben 6 (SoSe 12)
Inhaltsverzeichnis |
Aufgaben zum Abstand und zur Anordnung
Aufgabe 6.1
Definieren Sie: Strecke, Länge einer Strecke, die Halbgerade  und die Halbgerade
und die Halbgerade  . Suchen Sie verschiedene Schreibweisen. (Hilfe finden Sie im Skript "Abstand, Anordnung, Strecke".)
. Suchen Sie verschiedene Schreibweisen. (Hilfe finden Sie im Skript "Abstand, Anordnung, Strecke".)
Lösung von Aufgabe 6.1_S (SoSe_12)
Aufgabe 6.2
Warum ist die folgende Aufgabenstellung sinnlos?
Beweisen Sie Axiom II.2: Für beliebige Punkte  und
und  gilt:
gilt:  =
= 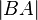
Lösung von Aufgabe 6.2_S (SoSe_12)
Aufgabe 6.3
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
Lösung von Aufgabe 6.3_S (SoSe_12)
Aufgabe 5.2
Diese Aufgabe war letzte Woche noch zu schwer- sorry dafür. Versuchen Sie es diese Woche nochmal.
Zeigen Sie, dass für drei paarweise verschiedene Punkte  und
und  gilt:
gilt:





Tipps zu Aufgabe 5.2 (SoSe_12)
Lösung von Aufgabe 5.2 (SoSe_12)
Aufgabe 5.4
Wie bei 5.2: Versuchen Sie es diese Woche nochmal.
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  auf
auf  mit
mit 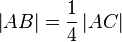 und
und 


Tipps zu Aufgabe 5.4 (SoSe_12)
Lösung von Aufgabe 5.4 (SoSe_12)
Aufgabe zur Inzidenz
Zusatzaufgabe 6.1
Es sei  eine Gerade und
eine Gerade und  ein Punkt, der nicht zu
ein Punkt, der nicht zu  gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene
gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene  , die sowohl alle Punkte von
, die sowohl alle Punkte von  als auch den Punkt
als auch den Punkt  enthält.
enthält.
Lösung von Zusatzaufgabe 6.1_S (SoSe_12)
Aufgaben zum Abstand und zur Anordnung
Zusatzaufgabe 6.2
Im Skript steht als Beweis "trivial". Führen Sie die Beweise trotzdem mal durch. Gehen Sie kleinschrittig und gut begründet vor.
Beweisen Sie:
a) 

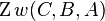
b) 

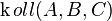
Lösung von Zusatzaufgabe 6.2_S (SoSe_12)
Zusatzaufgabe 6.3
a) Definieren Sie windschief auf der Menge aller Geraden (d.h.im Raum) auf zwei verschiedene Arten.
b) Warum ist die folgende Definition sinnlos?
- Zwei Ebenen sind windschief, wenn sie sich nicht schneiden und sie nicht parallel zueinander sind.
- Zwei Ebenen sind windschief, wenn sie sich nicht schneiden und sie nicht parallel zueinander sind.

