Serie 12 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 11.07) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 12.10) |
||
| (18 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
==Aufgabe 12.01== | ==Aufgabe 12.01== | ||
| − | <br /> | + | Mark definiert: Es sei <math>\overline{ABC}</math> ein rechtwinkliges Dreieck. Die längste Seite von <math>\overline{ABC}</math> heißt Hypotenuse von <math>\overline{ABC}</math>. <br /> Diskutieren Sie Marks Definition.<br /> |
[[Lösung von Aufgabe 12.01_SoSe_13]] | [[Lösung von Aufgabe 12.01_SoSe_13]] | ||
==Aufgabe 12.02 == | ==Aufgabe 12.02 == | ||
| + | Definieren Sie die Begriffe Kreistangente, Berührungspunkt einer Kreistangente und Berührungsradius einer Kreistangente. | ||
<br /> | <br /> | ||
[[Lösung von Aufg. 12.02_SoSe_13]] | [[Lösung von Aufg. 12.02_SoSe_13]] | ||
==Aufgabe 12.03 == | ==Aufgabe 12.03 == | ||
| + | Alles in ein und derselben Ebene: <br />Es sei <math>k</math> ein Kreis mit dem Mittelpunkt <math>M</math>. Ferner seien <math>B</math> ein Punkt von <math>k</math> und <math>t</math> eine Gerade durch <math>B</math>, die senkrecht auf <math>\overline{MB}</math> steht. Beweisen Sie: <math>t</math> ist Tangente an <math>k</math> im Punkt <math>B</math>. | ||
<br /> | <br /> | ||
[[Lösung von Aufg. 12.03_SoSe_13]] | [[Lösung von Aufg. 12.03_SoSe_13]] | ||
== Aufgabe 12.04 == | == Aufgabe 12.04 == | ||
| − | + | Die Gerade <math>t</math> sei Tangente an den Kreis <math>k</math> (Mittelpunkt <math>M</math>) im Punkt <math>B</math>. Beweisen Sie: <math>t \perp \overline{MB}</math>. | |
[[Lösung von Aufg. 12.04_SoSe_13]] | [[Lösung von Aufg. 12.04_SoSe_13]] | ||
==Aufgabe 12.05 == | ==Aufgabe 12.05 == | ||
| + | Definieren Sie den Begriff Inkreis eines Dreiecks unter der Verwendung des Begriffs Tangente. | ||
<br /> | <br /> | ||
[[Lösung von Aufg. 12.05_SoSe_13]] | [[Lösung von Aufg. 12.05_SoSe_13]] | ||
== Aufgabe 12.06 == | == Aufgabe 12.06 == | ||
| + | Beweisen Sie: Die Winkelhalbierenden eines Dreiecks <math>\overline{ABC}</math> schneiden sich in genau einem Punkt <math>S</math>, welcher der Mittelpunkt des Inkreises von <math>\overline{ABC}</math> ist. | ||
<br /> | <br /> | ||
| Zeile 31: | Zeile 35: | ||
==Aufgabe 12.07 == | ==Aufgabe 12.07 == | ||
| + | Definieren Sie den Begriff der Höhen eines Dreiecks. | ||
<br /> | <br /> | ||
[[Lösung von Aufg. 12.07_SoSe_13]] | [[Lösung von Aufg. 12.07_SoSe_13]] | ||
| − | ==Aufgabe | + | ==Aufgabe 12.08 == |
| − | + | Beweisen Sie: Die Höhen eines Dreiecks schneiden sich in genau einem Punkt. Das folgende Applet hilft:<br /> | |
| + | <ggb_applet width="755" height="502" version="3.2" ggbBase64="UEsDBBQACAAIADg68DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VhLc6M4ED7v/AoVh71FAfEw1NqZijOXVGUnU5XZOexNBhlrA4hFIhPn129LAgzOazybzE7WBwOtllr9ff0QzN/flgW6YY3kolo4HnYdxKpUZLzKF06r1kex8/7k3TxnImerhqK1aEqqFo6PiaPlLT9598tcbsRXRAuj8oWzrwtnTQvJHCTrhtFMbhhTEzltb3nBabO9XP3FUiV3A3aR86puwYpqWpClZXbBZf94bAzWBVcf+A3PWIMKkS6cKIStw90X1iie0mLhBK6VkIVD9gZB5OvRjWj4naiUVt8tvgYJQpLfMZjpWlkqKvmpEepMFG1ZSYRSUbjDBkXhje7J6N4fPIOHYDQQ9gOT5QWMoFYyMCMa2atreC+rYrsEMK9rwasdYJPZH+kNz6kCKpe0MbP6FeqCbpetUprkneQDg7+O9RrmTzX0qleK1Qsn0Wbmx4bsOWvTgmecVppQwwUAhdBXnqnNwpmFIcDKeL4BvoIw6DcomuxqKxUr0e2frBFg1I8xicMk9pOAJLMgjB20tUOhi0NC3JkbBXFAYk8vKYE1oMOHvQaRG0VeSJJwNotg0qNDxjS7uWJKQThLRG/ZLtDyhmeTh3O5FMVOZGA+o7VqG5MLfie6UlttDRBrtJOnVV6wTkYAsw1Lr1fi9soEj+fbpT9vazPFbGiVG3JRo8MSPMu768pejY7e6aDlGh3XaHRr6EWHcS8hRsNcV/ZqtApe2a11nnu9157bm+ESaYHrdNHSOV/QFYOUcFBbcXXRP0DqXHeuenbCx7ZcsSFOp2t6L7Xm/Hgv5ObXrKlY0UU+cNuKVqIbncSjpMhYykt4tAMdJFTT9QdswEozljes37itPBYwM+qOg3dPPD/uN2GyD/aa6rwDf5T2RVc4BdVl4ZQ4xw7KqNJSnT4FKxnUF2ViwoTUgM2pMxRTYepin4rd+A5lGH4wPkwk0aLeUJDgzgFIcqiSY5fMepfrtWQK3S6cowCwh0Jw5I2GfxfZFAdaAZ7GSWmqgos1YzVjlmzVBbmpLCZlJhUKMJTalo/9wBoLcAR3d7b+GC2bYLqcGLt+x75F7Bnslj8Uu1cCJ8EBseCE5u6lwDn7P4Azg37RhSn0h8PASUVZ0ipDFS3B1CdRbHNRGVC4Pmkg6ursQ9TTgYQo0ZBZPFrVj0PxKaC6e1YttWoULtDjV9ZgZ+YBNqzBHu9hqWmZVhuohhWT0vQSNe4aj3M3wmpMnhf6hr7Q6xrHjj3vEPYeDzHJcv00bCR9CW8ejsQnnDkwFHfh5OJZ7I5/NvMi7MYmtkiIIzdMdr94v6s+4SD7u7I60vY2XsKBNeVqCKpCB/p5paDTMdM57jewa8ZqfXK4rD43tJL65G11Ro3xG6mhb4uaIx8nNtMJ9vxk/Jv13ID83jHn7RCyeluE+Njz9mnYWp6CSQ7Zhn5EYjxziT/W/4mpmjaHC9jjXmc460v+fkvIni772t2BrewVi/30FeEHFEcfh5E/Cok4eCGCD+Kl69j0Hi/sAF7YW+Ll2croYzeJRjlJXirzDiJmaYlZ3SNmfQAx67dEzKEVMoQMC8KX6mCPkzOUyT2G1pah7B5Dp7/SWsjfnjvPTl5buynf0630K2BuLyt7+fdckCTAQeLFbve6AFhHUKF2PIT2EEGwG5D4e14gHkM1s6iye6guD0d1+bOhGuEg9PyoB7H/ZBBh3/Oi2RD9wWuBu34M3LPDwT37L8DdfXAhvgGP+N8GvUegWiRBGAwVv8M+jjEJwnAoPdHh2B+PP1+Zr7zdp/6TfwBQSwcIXHee3zkFAAAcGAAAUEsBAhQAFAAIAAgAODrwPFx3nt85BQAAHBgAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAABzBQAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /><br /> | ||
| + | Hinweis: Ein Klick auf den Button Rechts unten liefert die Konstruktionsbeschreibung.<br /> | ||
| − | [[Lösung von Aufgabe | + | [[Lösung von Aufgabe 12.08_SoSe_13]] |
| − | ==Aufgabe | + | ==Aufgabe 12.09 == |
| − | + | Informieren Sie sich, was Peripheriewinkel (Umfangswinkel) und Zentriwinkel (Mittelpunktswinkel) sind und definieren Sie diese Begriffe. | |
| − | [[Lösung von Aufgabe | + | <br /> |
| + | [[Lösung von Aufgabe 12.09_SoSe_13]] | ||
| − | ==Aufgabe | + | ==Aufgabe 12.10== |
| − | + | Formulieren Sie den Satz des Thales in Wenn-Dann-Form und beweisen sie ihn.<br /> | |
| − | + | [[Lösung von Aufgabe 12.10_SoSe_13]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[Lösung von Aufgabe | + | |
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Aktuelle Version vom 18. Juli 2013, 23:09 Uhr
Aufgabe 12.01Mark definiert: Es sei Aufgabe 12.02Definieren Sie die Begriffe Kreistangente, Berührungspunkt einer Kreistangente und Berührungsradius einer Kreistangente.
Aufgabe 12.03Alles in ein und derselben Ebene: Aufgabe 12.04Die Gerade Lösung von Aufg. 12.04_SoSe_13 Aufgabe 12.05Definieren Sie den Begriff Inkreis eines Dreiecks unter der Verwendung des Begriffs Tangente.
Aufgabe 12.06Beweisen Sie: Die Winkelhalbierenden eines Dreiecks Lösung von Aufg. 12.06_SoSe_13 Aufgabe 12.07Definieren Sie den Begriff der Höhen eines Dreiecks.
Aufgabe 12.08Beweisen Sie: Die Höhen eines Dreiecks schneiden sich in genau einem Punkt. Das folgende Applet hilft: Hinweis: Ein Klick auf den Button Rechts unten liefert die Konstruktionsbeschreibung. Lösung von Aufgabe 12.08_SoSe_13 Aufgabe 12.09Informieren Sie sich, was Peripheriewinkel (Umfangswinkel) und Zentriwinkel (Mittelpunktswinkel) sind und definieren Sie diese Begriffe.
Aufgabe 12.10Formulieren Sie den Satz des Thales in Wenn-Dann-Form und beweisen sie ihn. |
 ein rechtwinkliges Dreieck. Die längste Seite von
ein rechtwinkliges Dreieck. Die längste Seite von  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Ferner seien
. Ferner seien  ein Punkt von
ein Punkt von  eine Gerade durch
eine Gerade durch  steht. Beweisen Sie:
steht. Beweisen Sie: 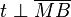 .
.
 , welcher der Mittelpunkt des Inkreises von
, welcher der Mittelpunkt des Inkreises von 
