Übung Aufgaben 5 P (SoSe 12)

Aufgabe 5.1

Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 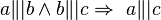$\ a \|| b \wedge b \|| c \Rightarrow \ a \|| c$ .
b) Welche Eigenschaft der Relation $\||$ auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
Lösung von Aufgabe 5.1P (SoSe_12)

Aufgabe 5.2

Eine informelle Definition:

Definition: Halbgerade $AB^+$

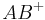Gegeben seien zwei verschiedene Punkte $\ A$ und $\ B$. Unter dem Strahl bzw. der Halbgeraden $\ AB^+$ versteht man die Strecke $\overline{AB}$ vereinigt mit der Menge aller der Punkte, die man erhält, wenn man $\overline{AB}$ über $\ B$ hinaus verlängert.

Formulieren Sie eine formal korrekte Definition des Begriffs Halbgerade 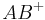$\ AB^+$.

Lösung von Aufg. 5.2P (SoSe_12)

Aufgabe 5.3

Definition: Halbgerade $AB^-$

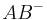Gegeben seien zwei nicht identische Punkte $\ A$ und $\ B$. Unter $\ AB^-$ wollen wir die Menge aller Punkte $\ P$ verstehen, die man erhält, wenn man $\overline{AB}$ über $\ A$ hinaus verlängert.

Geben Sie eine formal korrekte Definition für die Menge dieser Punkte $\ P$ an.

Lösung von Aufg. 5.3P (SoSe_12)

Aufgabe 5.4

Definieren Sie den Begriff: "konvexe Punktmenge".

Lösung von Aufg. 5.4P (SoSe_12)

Aufgabe 5.5

Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.

Lösung von Aufg. 5.5P (SoSe_12)

Aufgabe 5.6

Formulieren Sie die Kontraposition der Implikation aus Aufgabe 5.5.

Lösung von Aufg. 5.6P (SoSe_12)

Aufgabe 5.7

Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 5.5 nicht wahr ist.

Lösung von Aufg. 5.7P (SoSe_12)