Übung 6
Inhaltsverzeichnis |
Aufgaben zur Inzidenz
Aufgabe 6.1
Es sei  eine Gerade und
eine Gerade und  ein Punkt, der nicht zu
ein Punkt, der nicht zu  gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene
gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene  , die sowohl alle Punkte von
, die sowohl alle Punkte von  als auch den Punkt
als auch den Punkt  enthält.
enthält.
Aufgabe 6.2
Das Axiom I.7 sagt aus:
Es gibt vier Punkte, die nicht komplanar sind.
Es sei  eine beliebige Ebene und
eine beliebige Ebene und  die vier Punkte entsprechend Axiom I.7. Klassifizieren Sie alle Fälle die bezüglich der Inzidenz der Punkte
die vier Punkte entsprechend Axiom I.7. Klassifizieren Sie alle Fälle die bezüglich der Inzidenz der Punkte  mit
mit  auftreten können.
auftreten können.
Aufgabe 6.3
Satz:
- Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.
- Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
- Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
- Beweisen Sie den Satz. Hier ein Anfang für den Beweis:
Beweis
- Es seien
 und
und 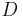 drei Punkte, die nicht komplanar sind.
drei Punkte, die nicht komplanar sind.
- Es seien
zu zeigen
- ...
Annahme:
- Es gibt drei der Punkte vier Punkte
 , die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...
, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...
- Es gibt drei der Punkte vier Punkte
Aufgabe 6.4 (*)
Beweisen Sie: Jede Ebene enthält wenigstens drei paarweise verschiedene Punkte.
Aufgaben zum Abstand
Aufgabe 6.5
Eine informelle Definition:
Definition: Halbgerade 
- Gegeben seien zwei verschiedene Punkte
 und
und  . Unter dem Strahl bzw. der Halbgeraden
. Unter dem Strahl bzw. der Halbgeraden 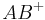 versteht man die Strecke
versteht man die Strecke  vereinigt mit der Menge aller der Punkte, die man erhält, wenn man
vereinigt mit der Menge aller der Punkte, die man erhält, wenn man  über
über  hinaus verlängert.
hinaus verlängert.
- Gegeben seien zwei verschiedene Punkte
Formulieren Sie eine mathematisch korrekte Definition des Begriffs Halbgerade 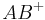 .
.
Aufgabe 6.6
Gegeben seien zwei nicht identische Punkte  und
und  . Unter
. Unter 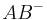 wollen wir die Menge aller Punkte
wollen wir die Menge aller Punkte  verstehen, die man erhält, wenn man
verstehen, die man erhält, wenn man  über
über  hinaus verlängert. Geben Sie eine mathematisch korrekte Definition für die Menge dieser Punkte
hinaus verlängert. Geben Sie eine mathematisch korrekte Definition für die Menge dieser Punkte  an.
an.
Aufgabe 6.7
Definieren Sie, was man unter einem Kreis  mit dem Mittelpunkt
mit dem Mittelpunkt  versteht. (Bezüglich der Definition wollen wir davon ausgehen, dass wir Geometrie im Raum betreiben.)
versteht. (Bezüglich der Definition wollen wir davon ausgehen, dass wir Geometrie im Raum betreiben.)
Aufgabe 6.8
Kreissehnen, Kreisradien und Kreisdurchmesser sind Strecken. Definieren Sie was man unter einer Sehne, einem Radius und einem Durchmesser eines Kreises versteht.
Aufgabe 6.9
Satz:
- Von drei paarweise verschiedenen Punkten
 und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
liegt genau einer zwischen den beiden anderen.
- Von drei paarweise verschiedenen Punkten
Beweisen Sie diesen Satz.
Lösung von Aufgabe 6.9 (Lösungsschema vorbereitet)
Aufgabe 6.10
Der folgende Satz bezieht sich auf die ebene Geometrie.
Satz:
- Es seien
 und
und  zwei Kreise mit den Mittelpunkten
zwei Kreise mit den Mittelpunkten  bzw.
bzw. 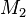 und den Radien
und den Radien 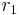 bzw.
bzw. 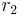 . Keiner der Mittelpunkte möge dabei im Inneren des jeweils anderen Kreises liegen.
. Keiner der Mittelpunkte möge dabei im Inneren des jeweils anderen Kreises liegen.
Die Kreise und
und  haben dann und nur dann einen und nur einen Punkt
haben dann und nur dann einen und nur einen Punkt  gemeinsam, wenn
gemeinsam, wenn 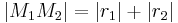 gilt.
gilt.
- Es seien
- Formulieren Sie den Satz ohne die Verwendung der Phrasen dann und nur dann sowie einen und nur einen.
- Sie haben sicherlich erkannt, dass es sich bei dem Satz um eine Äquivalenz handelt. Formulieren Sie die beiden Implikationen, die diese Äquivalenz beinhaltet.
- Bweisen Sie die beiden Implikationen.

