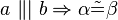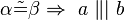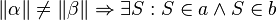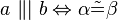Übung Aufgaben 2 P (SoSe 12): Unterschied zwischen den Versionen
(→Aufgabe 2.2) |
(→Aufgabe 2.2) |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /> | Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /> | ||
a) Wie lautet die Umkehrung des Basiswinkelsatzes?<br /> | a) Wie lautet die Umkehrung des Basiswinkelsatzes?<br /> | ||
| − | b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen ( | + | b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen (Kriterium). |
<br /> | <br /> | ||
[[Lösung von Aufgabe 2.2 (SoSe_12_P)]] | [[Lösung von Aufgabe 2.2 (SoSe_12_P)]] | ||
| Zeile 39: | Zeile 39: | ||
==Aufgabe 2.4== | ==Aufgabe 2.4== | ||
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).<br /> | a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).<br /> | ||
| − | b) Es seien ''a'' und ''b'' zwei nichtidentische Geraden, die durch eine dritte Gerade ''c'' jeweils in genau einem Punkt | + | b) Es seien ''a'' und ''b'' zwei nichtidentische Geraden, die durch eine dritte Gerade ''c'' jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel <math>\alpha </math> und <math>\beta </math>. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?<br /> |
#<math>\ a \ \|| \ b \Rightarrow \alpha \tilde {=} \beta </math> | #<math>\ a \ \|| \ b \Rightarrow \alpha \tilde {=} \beta </math> | ||
#<math>\alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b </math> | #<math>\alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b </math> | ||
Aktuelle Version vom 28. April 2012, 10:07 Uhr
Inhaltsverzeichnis |
Aufgaben zu Definitionen
Aufgabe 2.1
- Zur praktischen Motivierung der Beschäftigung mit welcher Vierecksart sind Scherenwagenheber (passende Bilder lassen sich leicht googlen) geeignet?
- Definieren Sie die Vierecksart, die Sie unter 1) genannt haben ohne auf einen Oberbegriff (außer Viereck) zurückzugreifen. Verwenden Sie für Ihre Definition die Eigenschaften der Diagonalen der zu definierenden Vierecksart.
- Definieren Sie die Vierecksart aus 1) noch zweimal unter Verwendung der unmittelbaren Oberbegriffe (Die Diagonaleigenschaften müssen jetzt keine Rolle in der Definition spielen).
- Aus rein geometrischer Sicht ist es für einen praktikablen Einsatz etwa zum Reifenwechsel hinreichend, Scherenwagenheber auf der Grundlage von Vierecken mit vier gleichlangen Seiten zu konstruieren. Allerdings ist die Verwendung dieser Vierecksart nicht notwendig für einen (aus rein geometrischer Sicht) funktionierenden Scherenwagenheber. Definieren Sie den Begriff des allgemeinen Wagenhebervierecks und ordnen Sie diesen in das Haus der Vierecke ein.
Lösung von Aufgabe 2.1 (SoSe_12_P)
Aufgaben zu Sätzen und Beweisen
Aufgabe 2.2
Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
a) Wie lautet die Umkehrung des Basiswinkelsatzes?
b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen (Kriterium).
Lösung von Aufgabe 2.2 (SoSe_12_P)
Aufgabe 2.3
Satz: In einem Dreieck  mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.
mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.
a) Welcher Beweis ist korrekt? Begründen Sie ausführlich! (Der Basiswinkelsatz und seine Umkehrung seien bereits bewiesen.)
Beweis 1)
Sei  ein Dreieck.
ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Da nach Voraussetzung |AC| ≠ |BC| gilt nach dem Basiswinkelsatz |α| ≠ |β|. Damit ist der Satz bewiesen.
Beweis 2)
Sei  ein Dreieck.
ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Nach Umkehrung des Basiswinkelsatzes gilt: Wenn |α|= |β| dann gilt |AC|= |BC|. Die Kontraposition der Umkehrung lautet also: Wenn |AC| ≠ |BC| dann gilt |α| ≠ |β|. Da die Kontraposition gleichwertig ist, kann man auch diese beweisen. Da nach Voraussetzung gilt: |AC|< |BC|, d.h. |AC| ≠ |BC|, kann nach Kontraposition der Umkehrung des Basiswinkelsatzes direkt gefolgert werden: |α| ≠ |β|. Damit ist der Satz bewiesen.
b) Beweisen Sie den Satz indirekt mit Widerspruch.
Lösung von Aufgabe 2.3 (SoSe_12_P)
Aufgabe 2.4
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel  und
und  . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
Lösung von Aufgabe 2.4 (SoSe_12_P)
Aufgabe 2.5
Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Lösung von Aufgabe 2.5 (SoSe_12_P)
Aufgabe 2.6
Es seine A und B zwei Punktmengen. Was müssen Sie konkret zeigen, wenn Sie beweisen wollen, dass A = B ?