Sommersemester 2012

Test

Einführung in die Geometrie

Haben wir nicht, bekommen wir auch nicht rein

Nürnberger_Trichter

Wöchentlich

• Auftrag der Woche_WS_11/12, Quiz der Woche_WS_11/12, Übungsaufgaben_WS_11/12 etc.‎

Materialien für das Studium

• Allgemeine Aspekte (Literatur, Ziele, Wiki, Vorgehensweise, Forschung)
• Einführendes Beispiel_WS_11/12
• Mengenlehre [Videos zur Mengenlehre]
• Definitionen in der Mathematik_WS_11/12
• Definitionen
• Sätze und Beweise WS_11/12
• Äquivalenzrelationen und Klasseneinteilungen WS_11/12
• Zusammenhang zwischen Äquivalenzrelationen und Klasseneinteilungen WS_11/12
• Einige grundlegende Aspekte zum Geometrieunterricht WS_11/12
• Eigenschaften von Geraden WS_11/12
• Übersicht: axiomatischer Aufbau der Geometrie
• Eigentlich ganz einfach und doch kompliziert: Punkte, Geraden WS_11/12
• Inzidenz im Raum WS_11/12)
• Strecken WS_11/12
• Streckenantragen oder das Axiom vom Lineal WS_11/12
• Halbebenen oder das Axiom von Pasch WS_11/12
• Winkel, Innere eines Winkels, Nebenwinkel, Scheitelwinkel WS_11/12
• Winkelmessung WS_11/12
• Mittelsenkrechte und Winkelhalbierende WS_11/12
• Dreieckskongruenz WS_11/12
• Basiswinkelsatz und Mittelsenkrechtenkriterium WS_11/12
• Der schwache Außenwinkelsatz WS_11/12
• Beziehungen zwischen den Seitenlängen und den Innenwinkelgrößen eines Dreiecks WS_11/12
• Das Lot von einem Punkt auf eine Gerade WS_11/12
• Umkehrung des Stufenwinkelsatzes WS_11/12
• Existenz von Parallelen und das Euklidische Parallelenaxiom WS_11/12
• Sätze über Dreiecke

• Innenwinkelsatz für Dreiecke und starker Außenwinkelsatz WS_11/12
• Dreieckstransversalen

• Der Umkreis und die Mittelsenkrechten eines Dreiecks WS_11/12
• Die Höhen eines Dreiecks WS_11/12
• Der Inkreis und die Winkelhalbierenden eines Dreiecks WS_11/12
• Der Schwerpunkt und die Seitenhalbierenden eines Dreiecks WS_11/12

• Sätze am Kreis

• Der Satz des Thales WS_11/12
• Sehnenvierecke und der Satz über die gegenüberliegenden Winkel im Sehnenviereck WS_11/12
• Peripheriewinkelsatz und Zentriwinkel-Peripheriewinkelsatz WS_11/12

Vorbereitung auf die Klausur zur ATP am 10.02.12

• Die Kraft der Raute
• Abstände und Parallelität

Videos

Videos von Studierenden

• Videos von Studierenden

Vorlesungsvideos

• Videos zur Mengenlehre
• Videos zur Einführung in die Geometrie

"Videobeweise"

• Der gefilmte Beweis SoSe_2011

Üben... Üben... Üben...

Aus den Übungen mit dem Classroompresenter (SoSe_2011)und Wintersemester 2011/12

Teilprüfungsklausuren der letzten Semester

Teilprüfungsklausur SoSe 10 mit Lösungen
Teilprüfungsklausur WS 10/11 mit Lösungen
Teilprüfungsklausur SoSe 11 mit Lösungen
Teilprüfungsklausur WS 11/12 ohne Lösungen
Teilprüfungsklausur WS 11/12 mit Lösungen |}

Aufgabe 1.1

In welchen Fällen handelt es sich um Definitionen? Begründen Sie!

1. Jedes n-Eck mit n=4 heißt Viereck.
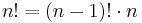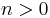
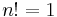2. $\ n!=(n-1)! \cdot n$, falls $\ n > 0$
   $\ n!=1$, falls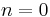 $\ n=0$
   
3. Stufenwinkel an geschnittenen Parallelen sind kongruent.
4. Jedes Dreieck mit einem Umkreis heißt Sehnendreieck.
5. Eine Gerade heißt Dreiecksschneidende, falls es ein Dreieck gibt, dessen drei Seiten von der Geraden geschnitten werden, wobei die Eckpunkte des Dreiecks nicht zur Geraden gehören.
6. Es gibt Vierecke mit einem Umkreis, die so genannten Sehnenvierecke.
7. Wenn ein n-Eck vier Ecken hat, dann ist es ein Viereck.
8. Jedes Viereck mit einem Umkreis heißt Sehnenviereck.
9. Es gibt Sehnenvierecke.
10. Punkt vor Strich.
11. Jeder Peripheriewinkel über einem Durchmesser ist ein Rechter.
12. Ein rechter Winkel ist ein solcher, der zu einem seiner Nebenwinkel kongruent ist.
13. Wenn ein Winkel zu einem seiner Nebenwinkel kongruent ist, so ist er ein Rechter.
14. Ein Viereck, das so aussieht wie die Vierecke auf der bayrischen Fahne, heißt Raute.
15. Es seien a und b zwei nichtidentische zueinander parallele Geraden. Lege auf a und b jeweils zwei verschiedene Punkte fest. Verbinde die vier Punkte zu einem konvexen Viereck. Du erhältst ein Trapez.
16. Die Menge aller Punkte, die von den Endpunkten einer Strecke ein und denselben Abstand hat, heißt Mittelsenkrechte der Strecke.
17. Eine Gerade, die senkrecht auf einer Strecke steht und diese halbiert, heißt Mittelsenkrechte der Strecke.
18. Ein Rechteck hat vier rechte Innenwinkel.
19. Ein Quadrat ist ein Rechteck.
20. Jedes Quadrat ist ein Rechteck.
21. Eine Raute ist ein Viereck mit vier gleich langen Seiten wobei je zwei Seiten parallel zueinander sind.

Lösung von Aufgabe 1.1 (WS_11_12)